3 Corrected parsimony

The phylogenetic dataset contains a considerable proportion of inapplicable codings (2240, = 24.9% of 9014 non-ambiguous tokens; 13.2% of 16992 total cells), which are known to introduce error and bias to phylogenetic reconstruction when the Fitch algorithm is employed (Brazeau et al., 2019; Maddison, 1993). As such, we used the R package TreeSearch v0.1.2 (Smith, 2018) to conduct phylogenetic tree search with a tree-scoring algorithm that avoids logically impossible character transformations when handling inapplicable data (Brazeau et al., 2019), implemented in the MorphyLib C library (Brazeau, Smith, & Guillerme, 2017).

3.1 Search parameters

Heuristic searches were conducted using the parsimony ratchet (Nixon, 1999) under equal and implied weights (Goloboff, 1997). The consensus tree presented in the main manuscript represents a strict consensus of all trees that are most parsimonious under one or more of the concavity constants (k) 3, 4.5, 7, 10.5, 16 and 24, an approach that has been shown to produce higher accuracy (i.e. more nodes and quartets resolved correctly) than equal weights at any given level of precision (Smith, 2019).

3.2 Analysis

The R commands used to conduct the analysis are reproduced below. The results can most readily be replicated using the R markdown files used to generate these pages: in Rstudio, run index.Rmd, then run each block in TreeSearch.Rmd. The complete analysis will take several hours.

3.2.1 Initialize and load data

# Load data from locally downloaded copy of MorphoBank matrix
my_data <- ReadAsPhyDat(nexusFile)
my_data[ignoredTaxa] <- NULL
iw_data <- PrepareDataIW(my_data)

3.2.2 Generate starting tree

Start by quickly rearranging a neighbour-joining tree, rooted on the outgroup.

nj.tree <- NJTree(my_data)
rooted.tree <- EnforceOutgroup(nj.tree, outgroup)
start.tree <- TreeSearch(tree=rooted.tree, dataset=my_data, maxIter=3000,
                         EdgeSwapper=RootedNNISwap, verbosity=0)

3.2.3 Implied weights analysis

The position of the root does not affect tree score, so we keep it fixed (using RootedXXXSwap functions) to avoid unnecessary swaps.

for (k in kValues) {
  iw.tree <- IWRatchet(start.tree, iw_data, concavity=k,
                       ratchHits = 20, ratchIter=4000, searchHits=56,
                       swappers=list(RootedTBRSwap, RootedSPRSwap, RootedNNISwap),
                       verbosity=0L)
  score <- IWScore(iw.tree, iw_data, concavity=k)
  # Write a single best tree
  write.nexus(iw.tree,
              file=paste0("TreeSearch/hk_iw_k", k, "_", 
                          signif(score, 5), ".nex", collapse=''))

  iw.consensus <- IWRatchetConsensus(iw.tree, iw_data, concavity=k,
                  swappers=list(RootedTBRSwap, RootedNNISwap),
                  searchHits=55, searchIter=4000, nSearch=250, verbosity=0L)
  write.nexus(iw.consensus,
              file=paste0("TreeSearch/hk_iw_k", k, "_", 
                          signif(IWScore(iw.consensus[[1]], iw_data, concavity=k), 5),
                          ".all.nex", collapse=''))
}

3.2.4 Equal weights analysis

ew.tree <- Ratchet(start.tree, my_data, verbosity=0L,
                   ratchHits = 20, ratchIter=4000, searchHits=55,
                   swappers=list(RootedTBRSwap, RootedSPRSwap, RootedNNISwap))
ew.consensus <- RatchetConsensus(ew.tree, my_data, nSearch=250, searchHits = 85,
                                 swappers=list(RootedTBRSwap, RootedNNISwap),
                                 verbosity=0L)
write.nexus(ew.consensus, file=paste0(collapse='', "TreeSearch/hk_ew_",
                                      Fitch(ew.tree, my_data), ".nex"))

3.3 Results

Optimal trees can be downloaded in Nexus format from github.com/ms609/halkieria/tree/master/TreeSearch.

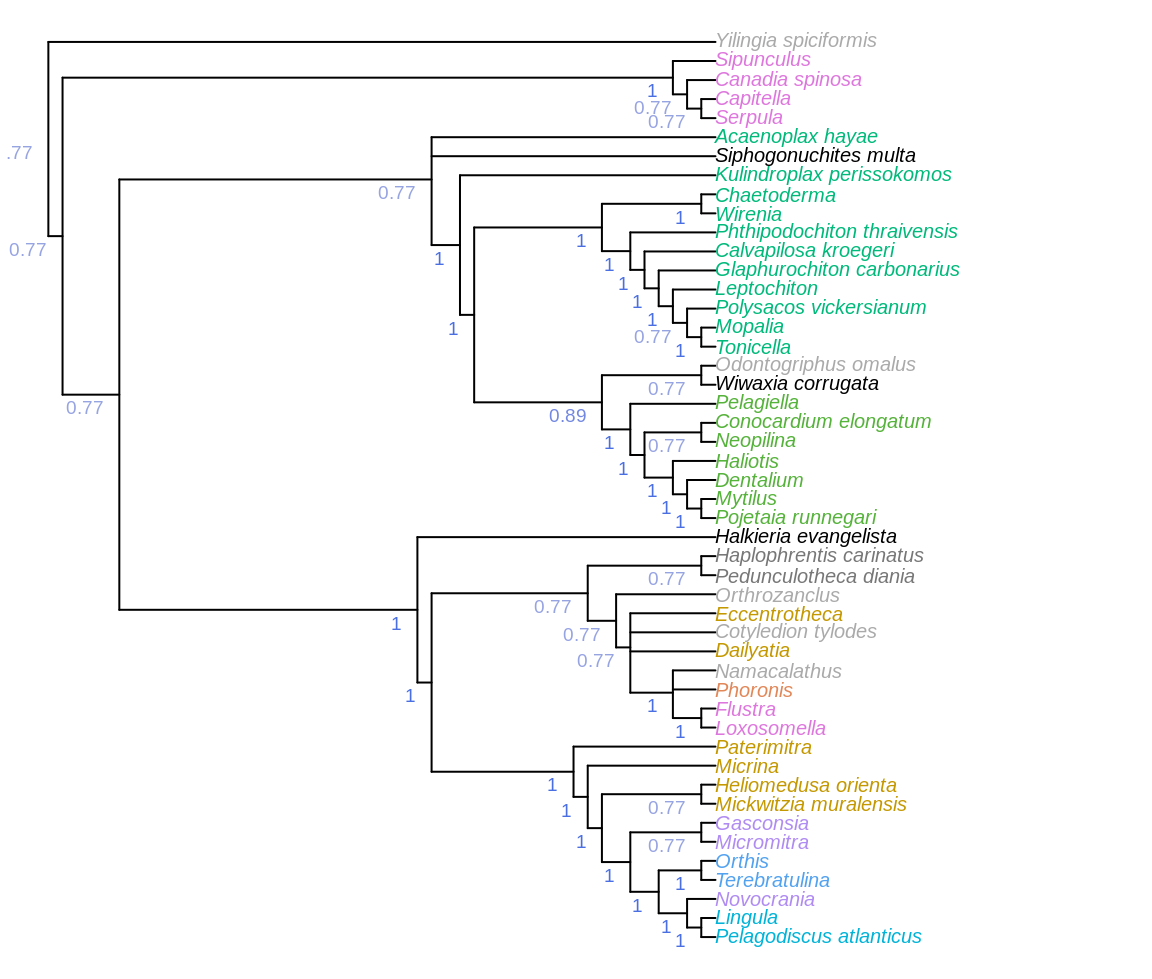
Figure 3.1: Consensus of all parsimony trees, under equal and implied weights. Node labels denote the frequency of each clade in most parsimonious trees under all analytical conditions.

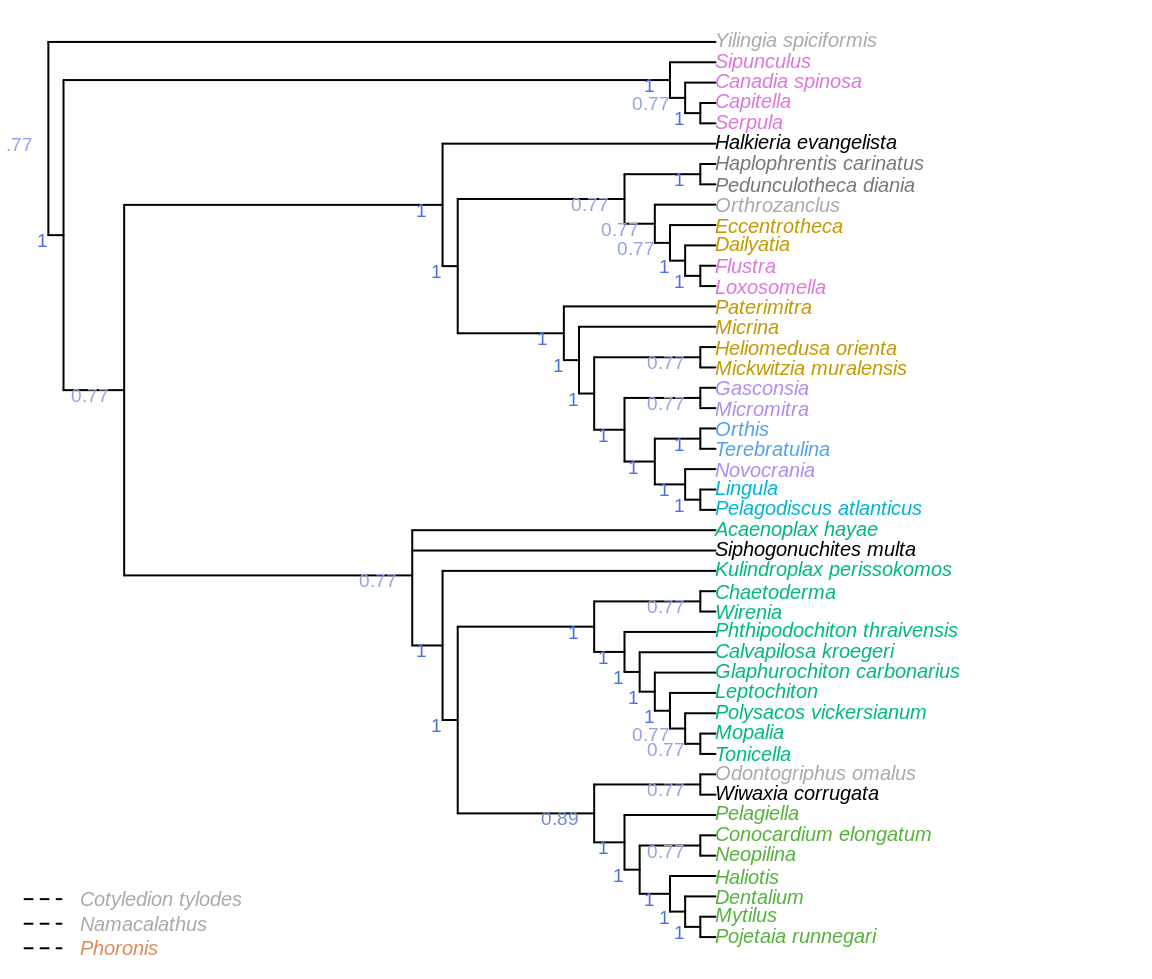
Figure 3.2: Consensus of same trees, with taxa pruned before constructing consensus to give context to clade support. Node labels denote the frequency of each clade in most parsimonious trees under all analytical conditions.

## 
##  > Results not available for panel 1

## 
##  > Results not available for panel 2

## 
##  > Results not available for panel 3

## 
##  > Results not available for panel 4

## 
##  > Results not available for panel 5

Figure 3.3: Strict consensus trees of implied weights analyses at k = 16 and 24.

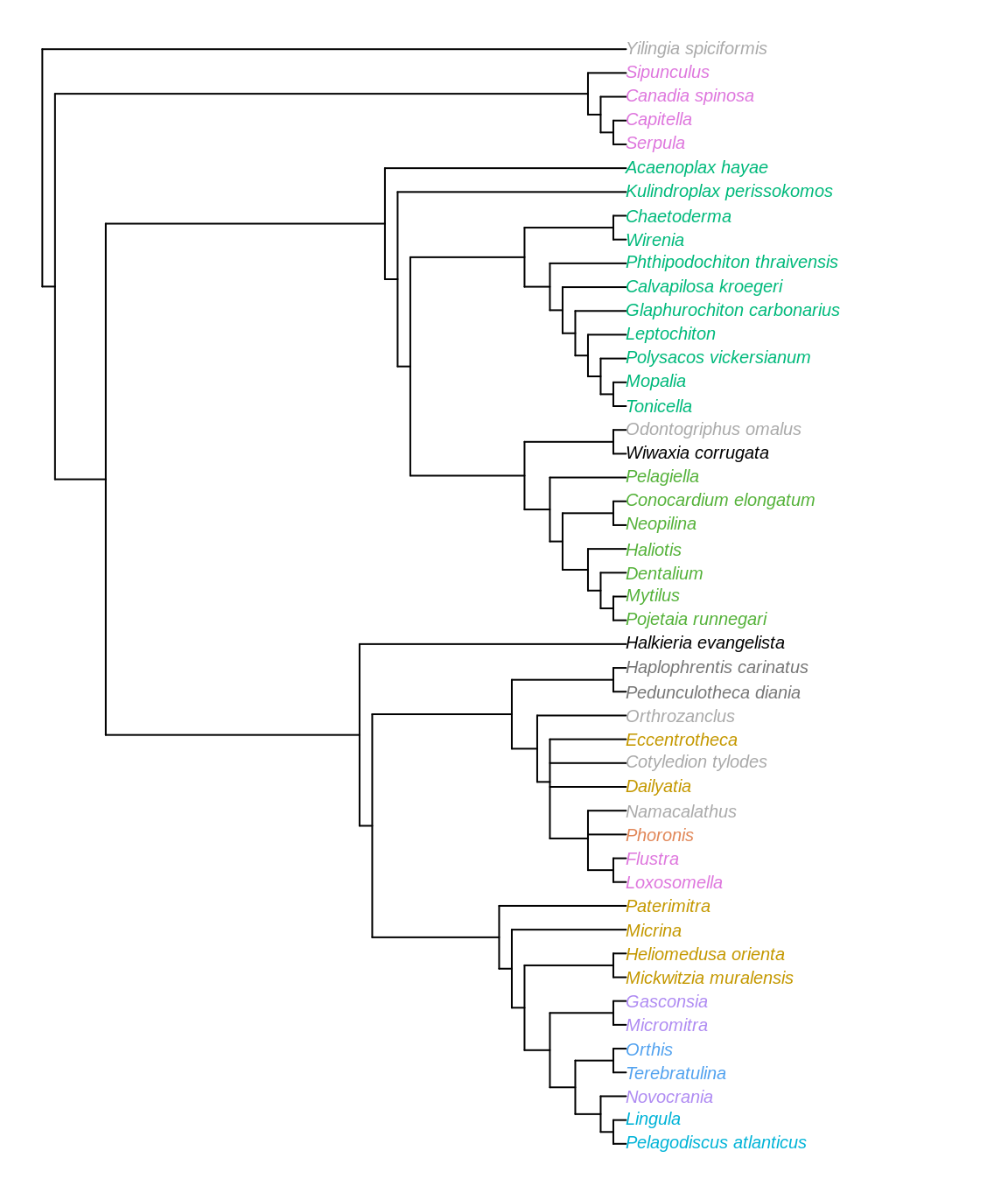
Figure 3.4: Strict consensus of most parsimonious trees under equally weighted parsimony

References

Brazeau, M. D., Guillerme, T., & Smith, M. R. (2019). An algorithm for morphological phylogenetic analysis with inapplicable data. Systematic Biology, online ahead of print. doi: 10.1093/sysbio/syy083

Brazeau, M. D., Smith, M. R., & Guillerme, T. (2017). MorphyLib: a library for phylogenetic analysis of categorical trait data with inapplicability. Zenodo. doi: 10.5281/zenodo.815371

Goloboff, P. A. (1997). Self-weighted optimization: tree searches and character state reconstructions under implied transformation costs. Cladistics, 13(3), 225–245. doi: 10.1111/j.1096-0031.1997.tb00317.x

Maddison, W. P. (1993). Missing data versus missing characters in phylogenetic analysis. Systematic Biology, 42(4), 576–581. doi: 10.1093/sysbio/42.4.576

Nixon, K. C. (1999). The Parsimony Ratchet, a new method for rapid parsimony analysis. Cladistics, 15(4), 407–414. doi: 10.1111/j.1096-0031.1999.tb00277.x

Smith, M. R. (2018). TreeSearch: Phylogenetic tree search using custom optimality criteria. doi: 10.5281/zenodo.1042590

Smith, M. R. (2019). Bayesian and parsimony approaches reconstruct informative trees from simulated morphological datasets. Biology Letters, 15(2), 20180632. doi: 10.1098/rsbl.2018.0632