Integer representing shape of a tree

Returns an integer that uniquely represents the shape of an n-tip binary tree, ignoring tip labels.

Usage

unrootedKeys

RootedTreeShape(tree)

RootedTreeWithShape(shape, nTip, tipLabels)

UnrootedTreeWithShape(shape, nTip, tipLabels = character(nTip))

UnrootedTreeWithKey(key, nTip, tipLabels = character(nTip))

UnrootedTreeShape(tree)

UnrootedTreeKey(tree, asInteger = FALSE)

.UnrootedKeys(nTip)

UnrootedKeys(..., envir = parent.frame())

NUnrootedShapes(nTip)

NRootedShapes(nTip)

Format

unrootedKeys is a list of length 22; each entry is a vector of integers corresponding to they keys (not shape numbers) of the different unrooted tree shapes with nTip leaves.

Arguments

tree: A tree of class phylo.
shape: Integer specifying shape of tree, perhaps generated by TreeShape().
nTip: Integer specifying number of tips.
tipLabels: Character vector listing the labels assigned to each tip in a tree, perhaps obtained using TipLabels().
key: Integer specifying the key (not number) of an unrooted tree.
asInteger: Logical specifying whether to coerce the return value to mode integer: only possible for values < 2^31. If FALSE, values will have class integer64.
...: Value of nTip, to pass to memoized .UnrootedKeys.
envir: Unused; passed to addMemoization().

Value

TreeShape() returns an integer specifying the shape of a tree, ignoring tip labels.

RootedTreeWithShape() returns a tree of class phylo corresponding to the shape provided. Tips are unlabelled.

UnrootedTreeWithShape() returns a tree of class phylo corresponding to the shape provided. Tips are unlabelled.

UnrootedTreeWithKey() returns a tree of class phylo corresponding to the key provided. Tips are unlabelled.

UnrootedKeys() returns a vector of integers corresponding to the keys (not shape numbers) of unrooted tree shapes with nTip tips. It is a wrapper to .UnrootedKeys(), with memoization, meaning that results once calculated are cached and need not be calculated on future calls to the function.

NUnrootedShapes() returns an object of class integer64 specifying the number of unique unrooted tree shapes with nTip (< 61) tips.

NRootedShapes() returns an object of class integer64 specifying the number of unique rooted tree shapes with nTip (< 56) leaves.

Details

Rooted trees are numbered working up from the root.

The root node divides n tips into two subtrees. The smaller subtree may contain $a = 1, 2, ..., n/2$ tips, leaving $b = n - a$ tips in These options are worked through in turn.

For the first shape of the smaller subtree, work through each possible shape for the larger subtree. Then, move to the next shape of the smaller subtree, and work through each possible shape of the larger subtree.

Stop when the desired topology is encountered.

Unrooted trees are numbered less elegantly. Each cherry (i.e. node subtending a pair of tips) is treated in turn. The subtended tips are removed, and the node treated as the root of a rooted tree. The number of this rooted tree is then calculated. The tree is assigned a key corresponding to the lowest such value. The keys of all unrooted tree shapes on n tips are ranked, and the unrooted tree shape is assigned a number based on the rank order of its key among all possible keys, counting from zero.

If UnrootedTreeShape() or UnrootedTreeKey() is passed a rooted tree, the position of the root will be ignored.

The number of unlabelled binary rooted trees corresponds to the Wedderburn-Etherington numbers.

Author

Martin R. Smith (martin.smith@durham.ac.uk)

Examples

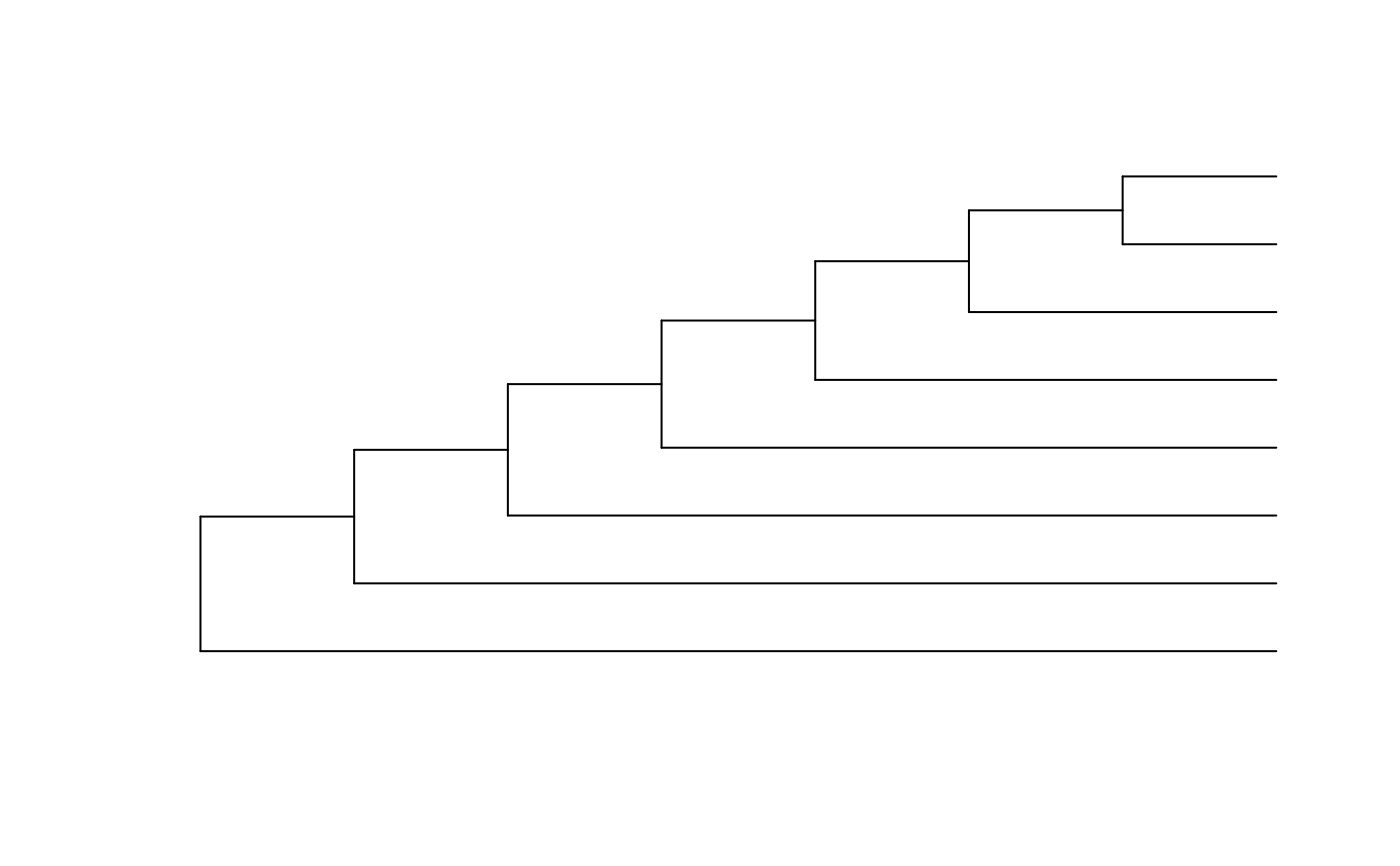
RootedTreeShape(PectinateTree(8))
#> integer64
#> [1] 0
plot(RootedTreeWithShape(0, nTip = 8L))


NRootedShapes(8L)
#> integer64
#> [1] 23
# Shapes are numbered from 0 to NRootedShapes(n) - 1.  The maximum shape is:
RootedTreeShape(BalancedTree(8))
#> integer64
#> [1] 22

# Unique shapes of unrooted trees:
NUnrootedShapes(8L)
#> integer64
#> [1] 4

# Keys of these trees:
UnrootedKeys(8L)
#> [1] 0 1 2 4

# A tree may be represented by multiple keys.
# For a one-to-one correspondence, use a number instead:
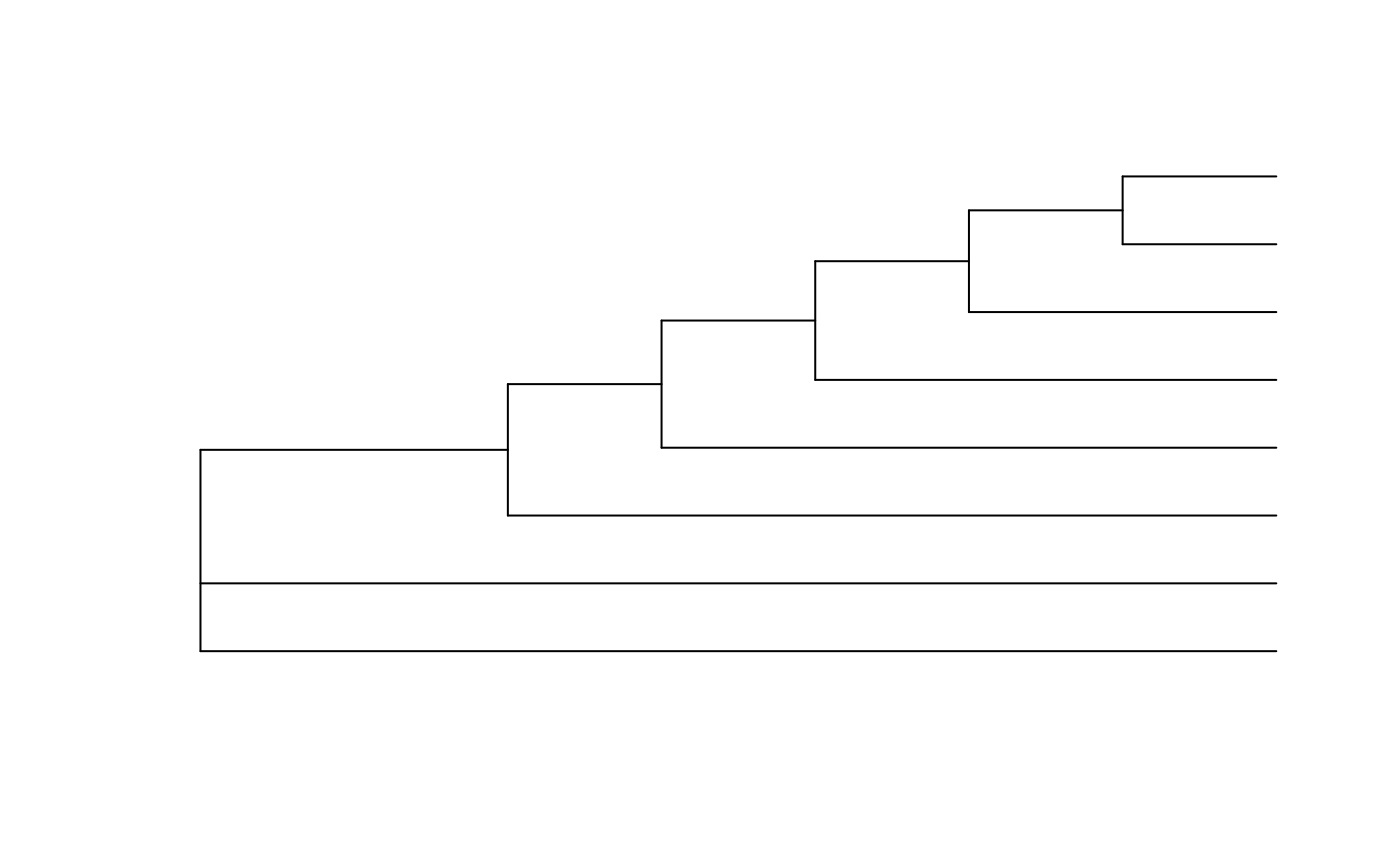
unrootedShapes8 <- as.integer(NUnrootedShapes(8L))
allShapes <- lapply(seq_len(unrootedShapes8) - 1L,
                    UnrootedTreeWithShape, 8L)
plot(allShapes[[1]])

sapply(allShapes, UnrootedTreeShape)
#> [1] 0 1 2 3
sapply(allShapes, UnrootedTreeKey, asInteger = TRUE) # Key >= number
#> [1] 0 1 2 4

# If numbers larger than 2>31 are required, sapply needs a little help
# with 64-bit integers:
structure(sapply(allShapes, UnrootedTreeKey), class = "integer64")
#> integer64
#> [1] 0 1 2 4