4 Bayesian analysis

Bayesian search was conducted in MrBayes v3.2.6 (Ronquist et al., 2012) using the Mk model (Lewis, 2001) with gamma-distributed rate variation across characters:

lset coding=variable rates=gamma;

Branch length was drawn from a dirichlet prior distribution, which is less informative than an exponential model (Rannala, Zhu, & Yang, 2012), but requires a prior mean tree length within about two orders of magnitude of the true value (C. Zhang, Rannala, & Yang, 2012). To satisfy this latter criterion, we specified the prior mean tree length to be equal to the length of the most parsimonious tree under equal weights, using a Dirichlet prior with \(\alpha_T = 1\), \(\beta_T = 1/(\)equal weights tree length\(/\)number of characters\()\), \(\alpha = c = 1\):

prset brlenspr = unconstrained: gammadir(1, 0.35, 1, 1);

Neomorphic and transformational characters (sensu Sereno, 2007) were allocated to two separate partitions whose proportion of invariant characters and gamma shape parameters were allowed to vary independently:

charset Neomorphic = 1 6 7 9 10 15 18 19 20 21 22 24 26 29 30 34 35 37 38 40 43 44 45 48 49 53 54 55 56 57 58 59 60 61 65 66 67 69 70 72 77 79 80 81 82 84 87 88 89 92 93 94 95 98 99 100 101 102 103 107 109 110 112 119 120 122 123 126 127 130 137 138 139 140 141 142 143 144 148 150 151 153 154 155 156 157 158 160 164 168 170 174 175 176 177 179 180 181 182 183 184 185 186 187 188 190 192 193 196 199 202 203 204 205 206 207 209 210 211 212 214 215 216 217 218 219 220 222 225;

charset Transformational = 2 3 4 5 8 11 12 13 14 16 17 23 25 27 28 31 32 33 36 39 41 42 46 47 50 51 52 62 63 64 68 71 73 74 75 76 78 83 85 86 90 91 96 97 104 105 106 108 111 113 114 115 116 117 118 121 124 125 128 129 131 132 133 134 135 136 145 146 147 149 152 159 161 162 163 165 166 167 169 171 172 173 178 189 191 194 195 197 198 200 201 208 213 221 223 224;

partition chartype = 2: Neomorphic, Transformational;

set partition = chartype;

unlink shape=(all) pinvar=(all);

Neomorphic characters were not assumed to have a symmetrical transition rate – that is, the probability of the absent → present transition was allowed to differ from that of the present → absent transition, being drawn from a uniform prior:

prset applyto=(1) symdirihyperpr=fixed(1.0);

The rate of variation in neomorphic characters was also allowed to vary from that of transformational characters:

prset applyto=(1) ratepr=variable;

Loxosomella was selected as an outgroup:

outgroup Loxosomella;

Four MrBayes runs were executed, each sampling eight chains for 5 000 000 generations, with samples taken every 500 generations. The first 10% of samples were discarded as burn-in.

mcmcp ngen=5000000 samplefreq=500 nruns=4 nchains=8 burninfrac=0.1;

A posterior tree topology was derived from the combined posterior sample of all runs. Convergence was indicated by PSRF = 1.00 and an estimated sample size of > 200 for each parameter. Nodes are labelled with posterior probabilities; recall that caution must be applied when interpreting these values (Z. Yang & Zhu, 2018).

The Nexus file used to generate these results in MrBayes can be downloaded, and run in MrBayes by typing exe path/to/download.

4.1 Parameter estimates

Parameter Mean Variance minESS avgESS PSRF
TL{all} 9.980 0.50100 5440 5970 0.99999
m{1} 0.462 0.00265 3100 3720 0.99999

4.2 Results

The posterior tree distribution can be downloaded in Nexus format from github.com/ms609/hyoliths/tree/master/MrBayes.

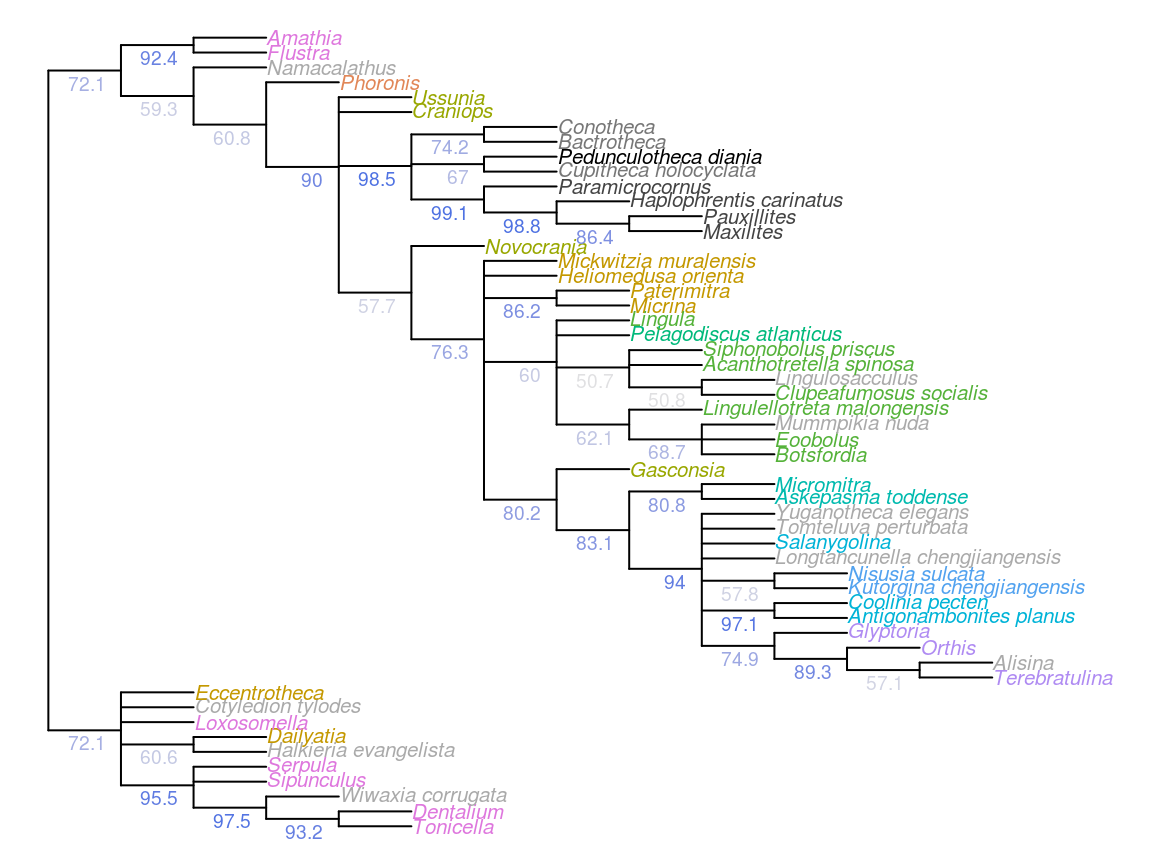
Results of Bayesian analysis, posterior probability > 50%, all taxa

Figure 4.1: Results of Bayesian analysis, posterior probability > 50%, all taxa

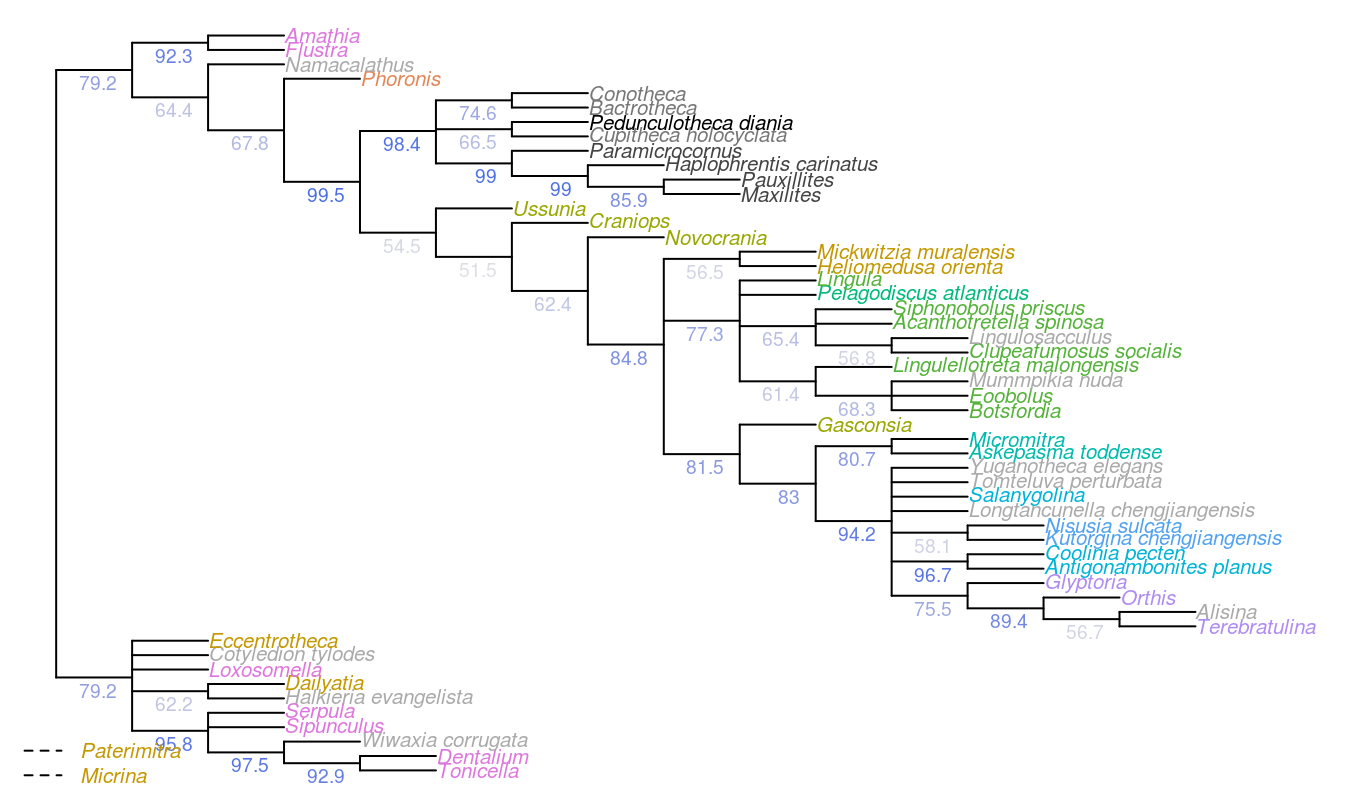
Results of Bayesian analysis, posterior probability > 50%, wildcard taxa pruned

Figure 4.2: Results of Bayesian analysis, posterior probability > 50%, wildcard taxa pruned

References

Ronquist, F., Teslenko, M., van der Mark, P., Ayres, D. L., Darling, A., Hohna, S., … Huelsenbeck, J. P. (2012). MrBayes 3.2: Efficient Bayesian phylogenetic inference and model choice across a large model space. Systematic Biology, 61(3), 539–42. doi:10.1093/sysbio/sys029

Lewis, P. O. (2001). A likelihood approach to estimating phylogeny from discrete morphological character data. Systematic Biology, 50(6), 913–925. doi:10.1080/106351501753462876

Rannala, B., Zhu, T.-Q., & Yang, Z.-H. (2012). Tail paradox, partial identifiability, and influential priors in Bayesian branch length inference. Molecular Biology and Evolution, 29(1), 325–335. doi:10.1093/molbev/msr210

Zhang, C., Rannala, B., & Yang, Z.-H. (2012). Robustness of compound Dirichlet priors for Bayesian inference of branch lengths. Systematic Biology, 61(5), 779–84. doi:10.1093/sysbio/sys030

Sereno, P. C. (2007). Logical basis for morphological characters in phylogenetics. Cladistics, 23(6), 565–587. doi:10.1111/j.1096-0031.2007.00161.x

Yang, Z., & Zhu, T. (2018). Bayesian selection of misspecified models is overconfident and may cause spurious posterior probabilities for phylogenetic trees. Proceedings of the National Academy of Sciences, 115(8), 1854–1859. doi:10.1073/pnas.1712673115