Calculate the Jaccard–Robinson–Foulds metric (Böcker et al. 2013) , a Generalized Robinson–Foulds metric.
Usage
JaccardRobinsonFoulds(
tree1,
tree2 = NULL,
k = 1L,
allowConflict = TRUE,
similarity = FALSE,
normalize = FALSE,
reportMatching = FALSE
)
JaccardSplitSimilarity(
splits1,
splits2,
nTip = attr(splits1, "nTip"),
k = 1L,
allowConflict = TRUE,
reportMatching = FALSE
)Arguments
- tree1, tree2
Trees of class
phylo, with leaves labelled identically, or lists of such trees to undergo pairwise comparison. Where implemented,tree2 = NULLwill compute distances between each pair of trees in the listtree1using a fast algorithm based on Day (1985) .- k
An arbitrary exponent to which to raise the Jaccard index. Integer values greater than one are anticipated by Böcker et al. The Nye et al. metric uses
k = 1. As k increases towards infinity, the metric converges to the Robinson–Foulds metric.- allowConflict
Logical specifying whether to allow conflicting splits to be paired. If
FALSE, such pairings will be allocated a similarity score of zero.- similarity
Logical specifying whether to report the result as a tree similarity, rather than a difference.
- normalize
If a numeric value is provided, this will be used as a maximum value against which to rescale results. If
TRUE, results will be rescaled against a maximum value calculated from the specified tree sizes and topology, as specified in the "Normalization" section below. IfFALSE, results will not be rescaled.- reportMatching
Logical specifying whether to return the clade matchings as an attribute of the score.
- splits1, splits2
Logical matrices where each row corresponds to a leaf, either listed in the same order or bearing identical names (in any sequence), and each column corresponds to a split, such that each leaf is identified as a member of the ingroup (
TRUE) or outgroup (FALSE) of the respective split.- nTip
(Optional) Integer specifying the number of leaves in each split.
Value
JaccardRobinsonFoulds() returns an array of numerics providing the
distances between each pair of trees in tree1 and tree2,
or splits1 and splits2.
Details
In short, the Jaccard–Robinson–Foulds metric is a generalized Robinson-Foulds metric: it finds the optimal matching that pairs each split in one tree with a similar split in the second. Matchings are scored according to the size of the largest split that is consistent with both of them, normalized against the Jaccard index, and raised to an arbitrary exponent. A more detailed explanation is provided in the vignettes.
By default, conflicting splits may be paired.
Note that the settings k = 1, allowConflict = TRUE, similarity = TRUE
give the similarity metric of Nye et al. (2006)
;
a slightly faster implementation of this metric is available as
NyeSimilarity().
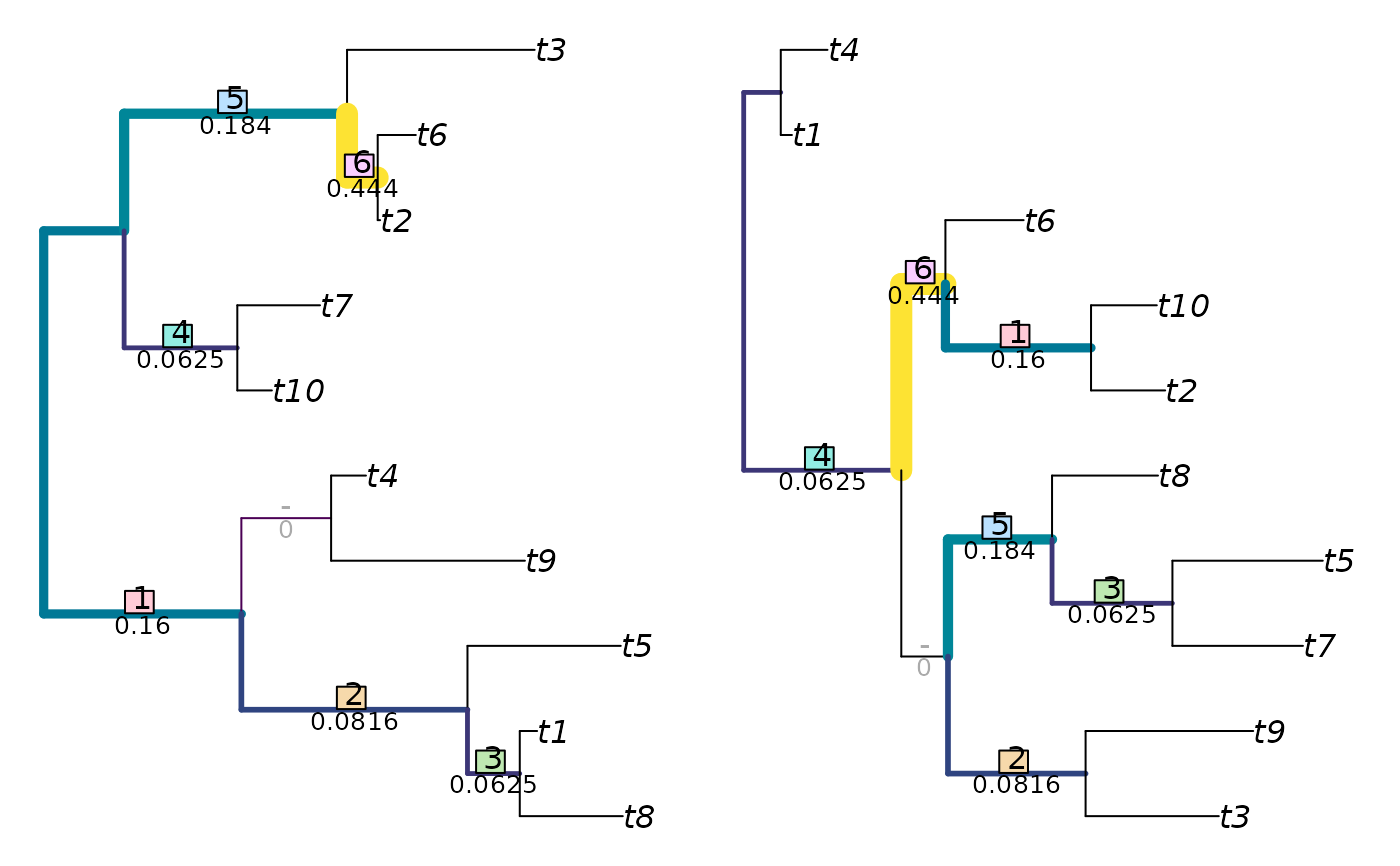
The examples section below details how to visualize matchings with non-default parameter values.
Trees need not contain identical leaves; scores are based on the leaves that
trees hold in common. Check for unexpected differences in tip labelling
with setdiff(TipLabels(tree1), TipLabels(tree2)).
Normalization
If normalize = TRUE, then results will be rescaled from zero to one by
dividing by the maximum possible value for trees of the given topologies,
which is equal to the sum of the number of splits in each tree.
You may wish to normalize instead against the maximum number of splits
present in a pair of trees with n leaves, by specifying
normalize = n - 3.
References
Böcker S, Canzar S, Klau GW (2013).
“The generalized Robinson-Foulds metric.”
In Darling A, Stoye J (eds.), Algorithms in Bioinformatics. WABI 2013. Lecture Notes in Computer Science, vol 8126, 156–169.
Springer, Berlin, Heidelberg.
doi:10.1007/978-3-642-40453-5_13
.
Day WHE (1985).
“Optimal algorithms for comparing trees with labeled leaves.”
Journal of Classification, 2(1), 7–28.
doi:10.1007/BF01908061
.
Nye TMW, Liò P, Gilks WR (2006).
“A novel algorithm and web-based tool for comparing two alternative phylogenetic trees.”
Bioinformatics, 22(1), 117–119.
doi:10.1093/bioinformatics/bti720
.
See also
Other tree distances:
HierarchicalMutualInfo(),
KendallColijn(),
MASTSize(),
MatchingSplitDistance(),
NNIDist(),
NyeSimilarity(),
PathDist(),
Robinson-Foulds,
SPRDist(),
TreeDistance()
Examples
set.seed(2)
tree1 <- ape::rtree(10)
tree2 <- ape::rtree(10)
JaccardRobinsonFoulds(tree1, tree2, k = 2, allowConflict = FALSE)
#> [1] 12.0105
JaccardRobinsonFoulds(tree1, tree2, k = 2, allowConflict = TRUE)
#> [1] 11.40222
JRF2 <- function(tree1, tree2, ...)
JaccardRobinsonFoulds(tree1, tree2, k = 2, allowConflict = FALSE, ...)
VisualizeMatching(JRF2, tree1, tree2, matchZeros = FALSE)