Matching Split Distance

Calculate the Matching Split Distance (Bogdanowicz and Giaro 2012; Lin et al. 2012) for unrooted binary trees.

Usage

MatchingSplitDistance(
  tree1,
  tree2 = NULL,
  normalize = FALSE,
  reportMatching = FALSE
)

MatchingSplitDistanceSplits(
  splits1,
  splits2,
  nTip = attr(splits1, "nTip"),
  normalize = TRUE,
  reportMatching = FALSE
)

Arguments

tree1, tree2

Trees of class phylo, with leaves labelled identically, or lists of such trees to undergo pairwise comparison. Where implemented, tree2 = NULL will compute distances between each pair of trees in the list tree1 using a fast algorithm based on Day (1985) .

normalize

If a numeric value is provided, this will be used as a maximum value against which to rescale results. If TRUE, results will be rescaled against a maximum value calculated from the specified tree sizes and topology, as specified in the "Normalization" section below. If FALSE, results will not be rescaled.

reportMatching

Logical specifying whether to return the clade matchings as an attribute of the score.

splits1, splits2

Logical matrices where each row corresponds to a leaf, either listed in the same order or bearing identical names (in any sequence), and each column corresponds to a split, such that each leaf is identified as a member of the ingroup (TRUE) or outgroup (FALSE) of the respective split.

nTip

(Optional) Integer specifying the number of leaves in each split.

Value

MatchingSplitDistance() returns an array of numerics providing the distances between each pair of trees in tree1 and tree2, or splits1 and splits2.

Details

Trees need not contain identical leaves; scores are based on the leaves that trees hold in common. Check for unexpected differences in tip labelling with setdiff(TipLabels(tree1), TipLabels(tree2)).

Normalization

A normalization value or function must be provided in order to return a normalized value. If you are aware of a generalised formula, please let me know by creating a GitHub issue so that it can be implemented.

References

Bogdanowicz D, Giaro K (2012). “Matching split distance for unrooted binary phylogenetic trees.” IEEE/ACM Transactions on Computational Biology and Bioinformatics, 9(1), 150–160. doi:10.1109/TCBB.2011.48 .

Day WHE (1985). “Optimal algorithms for comparing trees with labeled leaves.” Journal of Classification, 2(1), 7–28. doi:10.1007/BF01908061 .

Lin Y, Rajan V, Moret BME (2012). “A metric for phylogenetic trees based on matching.” IEEE/ACM Transactions on Computational Biology and Bioinformatics, 4(9), 1014–1022. doi:10.1109/TCBB.2011.157 .

See also

Other tree distances: HierarchicalMutualInfo(), JaccardRobinsonFoulds(), KendallColijn(), MASTSize(), NNIDist(), NyeSimilarity(), PathDist(), Robinson-Foulds, SPRDist(), TreeDistance()

Author

Martin R. Smith (martin.smith@durham.ac.uk)

Examples

MatchingSplitDistance(lapply(rep(8, 5), ape::rtree), normalize = 16)
#>       1     2     3     4
#> 2 0.750                  
#> 3 0.750 0.500            
#> 4 0.625 0.625 0.875      
#> 5 0.750 0.500 0.250 0.750

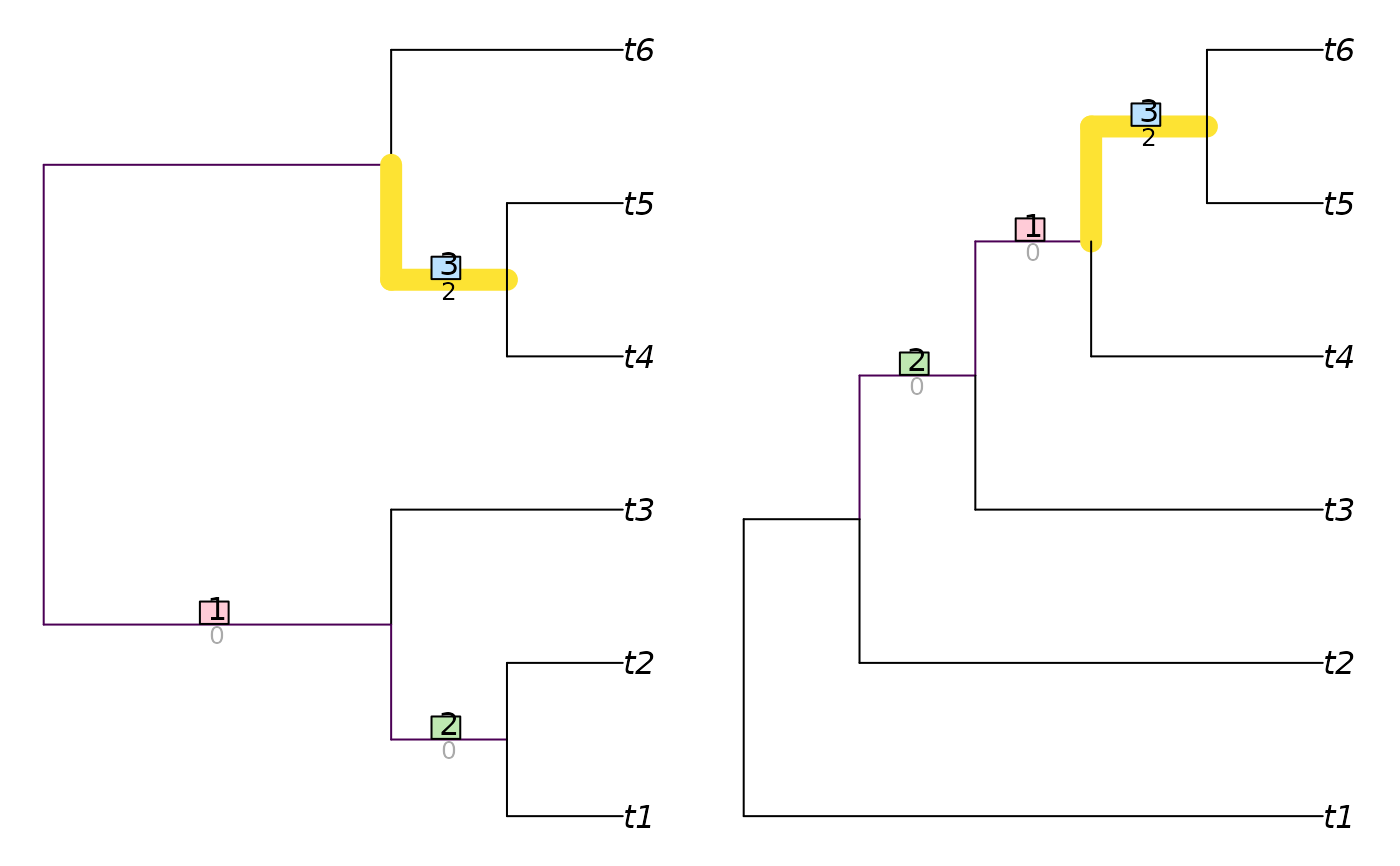
MatchingSplitDistance(TreeTools::BalancedTree(6),
                      TreeTools::PectinateTree(6),
                      reportMatching = TRUE)
#> [1] 2
#> attr(,"matching")
#> [1] 2 1 3
#> attr(,"matchedSplits")
#> [1] "t1 t2 t3 | t4 t5 t6 => t4 t5 t6 | t1 t2 t3"
#> [2] "t1 t2 | t3 t4 t5 t6 => t3 t4 t5 t6 | t1 t2"
#> [3] "t4 t5 | t1 t2 t3 t6 => t5 t6 | t1 t2 t3 t4"
#> attr(,"matchedScores")
#> [1] 0 0 2
#> attr(,"pairScores")
#>      [,1] [,2] [,3]
#> [1,]    1    0    1
#> [2,]    0    1    2
#> [3,]    2    1    2

VisualizeMatching(MatchingSplitDistance, TreeTools::BalancedTree(6),
                  TreeTools::PectinateTree(6))