Nye et al. (2006) tree comparison

NyeSimilarity() and NyeSplitSimilarity() implement the Generalized Robinson–Foulds tree comparison metric of Nye et al. (2006) . In short, this finds the optimal matching that pairs each branch from one tree with a branch in the second, where matchings are scored according to the size of the largest split that is consistent with both of them, normalized against the Jaccard index. A more detailed account is available in the vignettes.

Usage

NyeSimilarity(
  tree1,
  tree2 = NULL,
  similarity = TRUE,
  normalize = FALSE,
  normalizeMax = !is.logical(normalize),
  reportMatching = FALSE,
  diag = TRUE
)

NyeSplitSimilarity(
  splits1,
  splits2,
  nTip = attr(splits1, "nTip"),
  reportMatching = FALSE
)

Arguments

tree1, tree2

Trees of class phylo, with leaves labelled identically, or lists of such trees to undergo pairwise comparison. Where implemented, tree2 = NULL will compute distances between each pair of trees in the list tree1 using a fast algorithm based on Day (1985) .

similarity

Logical specifying whether to report the result as a tree similarity, rather than a difference.

normalize

If a numeric value is provided, this will be used as a maximum value against which to rescale results. If TRUE, results will be rescaled against a maximum value calculated from the specified tree sizes and topology, as specified in the "Normalization" section below. If FALSE, results will not be rescaled.

normalizeMax

When calculating similarity, normalize against the maximum number of splits that could have been present (TRUE), or the number of splits that were actually observed (FALSE)? Defaults to the number of splits in the better-resolved tree; set normalize = pmin.int to use the number of splits in the less resolved tree.

reportMatching

Logical specifying whether to return the clade matchings as an attribute of the score.

diag

Logical specifying whether to return similarities along the diagonal, i.e. of each tree with itself. Applies only if tree2 is a list identical to tree1, or NULL.

splits1, splits2

Logical matrices where each row corresponds to a leaf, either listed in the same order or bearing identical names (in any sequence), and each column corresponds to a split, such that each leaf is identified as a member of the ingroup (TRUE) or outgroup (FALSE) of the respective split.

nTip

(Optional) Integer specifying the number of leaves in each split.

Value

NyeSimilarity() returns an array of numerics providing the distances between each pair of trees in tree1 and tree2, or splits1 and splits2.

Details

The measure is defined as a similarity score. If similarity = FALSE, the similarity score will be converted into a distance by doubling it and subtracting it from the number of splits present in both trees. This ensures consistency with JaccardRobinsonFoulds.

Note that NyeSimilarity(tree1, tree2) is equivalent to, but slightly faster than, JaccardRobinsonFoulds (tree1, tree2, k = 1, allowConflict = TRUE).

Normalization

If normalize = TRUE and similarity = TRUE, then results will be rescaled from zero to one by dividing by the mean number of splits in the two trees being compared.

You may wish to normalize instead against the number of splits present in the smaller tree, which represents the maximum value possible for a pair of trees with the specified topologies (normalize = pmin.int); the number of splits in the most resolved tree (normalize = pmax.int); or the maximum value possible for any pair of trees with n leaves, n - 3 (normalize = TreeTools::NTip(tree1) - 3L).

If normalize = TRUE and similarity = FALSE, then results will be rescaled from zero to one by dividing by the total number of splits in the pair of trees being considered.

Trees need not contain identical leaves; scores are based on the leaves that trees hold in common. Check for unexpected differences in tip labelling with setdiff(TipLabels(tree1), TipLabels(tree2)).

References

Day WHE (1985). “Optimal algorithms for comparing trees with labeled leaves.” Journal of Classification, 2(1), 7–28. doi:10.1007/BF01908061 .

Nye TMW, Liò P, Gilks WR (2006). “A novel algorithm and web-based tool for comparing two alternative phylogenetic trees.” Bioinformatics, 22(1), 117–119. doi:10.1093/bioinformatics/bti720 .

See also

Other tree distances: JaccardRobinsonFoulds(), KendallColijn(), MASTSize(), MatchingSplitDistance(), NNIDist(), PathDist(), Robinson-Foulds, SPRDist(), TreeDistance()

Author

Martin R. Smith (martin.smith@durham.ac.uk)

Examples

library("TreeTools")
NyeSimilarity(BalancedTree(8), PectinateTree(8))
#> [1] 3.8
VisualizeMatching(NyeSimilarity, BalancedTree(8), PectinateTree(8))

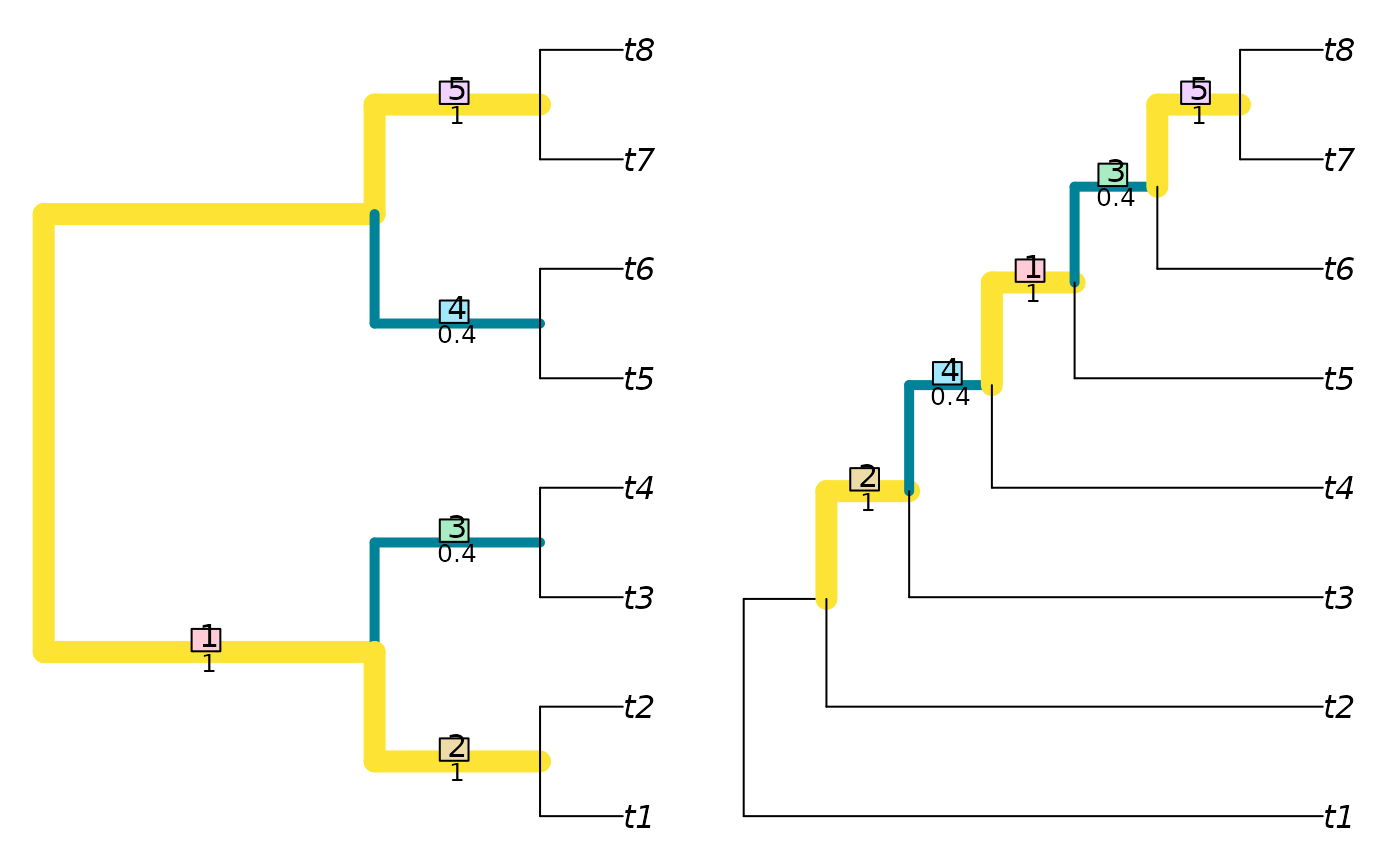NyeSimilarity(as.phylo(0:5, nTip = 8), PectinateTree(8))
#> [1] 3.166667 2.750000 2.750000 2.500000 2.450000 2.500000
NyeSimilarity(as.phylo(0:5, nTip = 8), similarity = FALSE)
#>          1        2        3        4        5
#> 2 1.333333                                    
#> 3 1.333333 1.333333                           
#> 4 2.166667 2.333333 2.333333                  
#> 5 2.333333 2.166667 2.333333 1.000000         
#> 6 2.000000 2.000000 1.500000 1.500000 1.500000