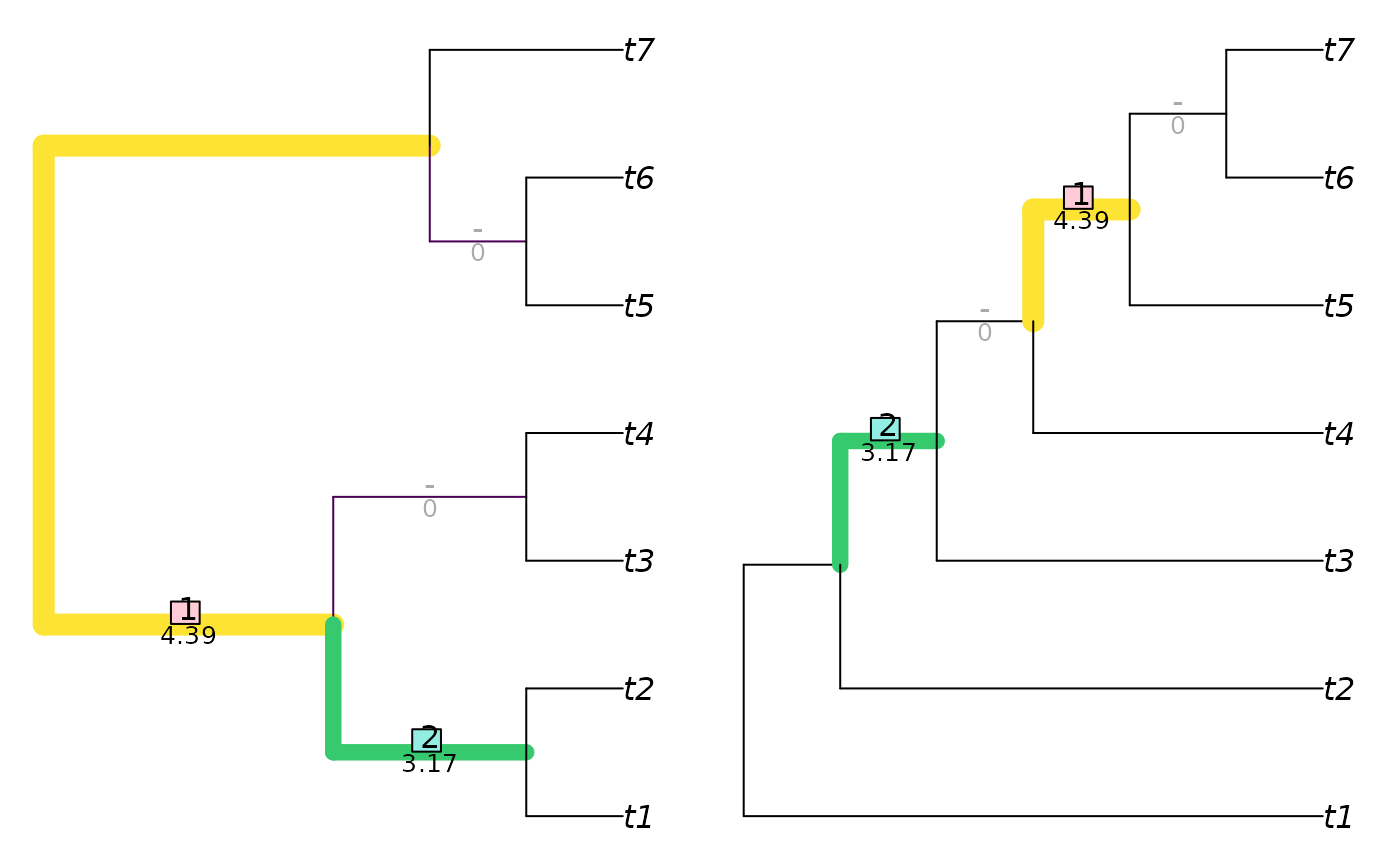Robinson–Foulds distances, with adjustments for phylogenetic information content
Source:R/tree_distance_rf.R
Robinson-Foulds.RdRobinsonFoulds() calculates the Robinson–Foulds distance
(Robinson and Foulds 1981)
, or the corresponding similarity measure.
InfoRobinsonFoulds() weights splits according to their phylogenetic
information content (§2.1 in Smith 2020)
.
Optionally, the matching between identical splits may reported.
Generalized Robinson–Foulds distances (see TreeDistance())
are better suited to most use cases
(Smith 2020, 2022)
.
Usage
InfoRobinsonFoulds(
tree1,
tree2 = NULL,
similarity = FALSE,
normalize = FALSE,
reportMatching = FALSE
)
InfoRobinsonFouldsSplits(
splits1,
splits2,
nTip = attr(splits1, "nTip"),
reportMatching = FALSE
)
RobinsonFoulds(
tree1,
tree2 = NULL,
similarity = FALSE,
normalize = FALSE,
reportMatching = FALSE
)
RobinsonFouldsMatching(
tree1,
tree2,
similarity = FALSE,
normalize = FALSE,
...
)
RobinsonFouldsSplits(
splits1,
splits2,
nTip = attr(splits1, "nTip"),
reportMatching = FALSE
)Arguments
- tree1, tree2
Trees of class
phylo, with leaves labelled identically, or lists of such trees to undergo pairwise comparison. Where implemented,tree2 = NULLwill compute distances between each pair of trees in the listtree1using a fast algorithm based on Day (1985) .- similarity
Logical specifying whether to report the result as a tree similarity, rather than a difference.
- normalize
If a numeric value is provided, this will be used as a maximum value against which to rescale results. If
TRUE, results will be rescaled against a maximum value calculated from the specified tree sizes and topology, as specified in the "Normalization" section below. IfFALSE, results will not be rescaled.- reportMatching
Logical specifying whether to return the clade matchings as an attribute of the score.
- splits1, splits2
Logical matrices where each row corresponds to a leaf, either listed in the same order or bearing identical names (in any sequence), and each column corresponds to a split, such that each leaf is identified as a member of the ingroup (
TRUE) or outgroup (FALSE) of the respective split.- nTip
(Optional) Integer specifying the number of leaves in each split.
- ...
Not used.
Value
RobinsonFoulds() and InfoRobinsonFoulds() return an array of numerics providing the
distances between each pair of trees in tree1 and tree2,
or splits1 and splits2.
If reportMatching = TRUE, the pairScores attribute
returns a logical matrix specifying whether each pair of splits is identical.
Details
RobinsonFoulds() calculates the standard Robinson–Foulds distance,
i.e. the number of splits that occur in one tree but not the other.
InfoRobinsonFoulds() calculates the tree similarity or distance by summing
the phylogenetic information content of all splits that are (or are not)
identical in both trees. Consequently, splits that are more likely
to be identical by chance alone make a smaller contribution to overall
tree distance, because their similarity is less remarkable.
Rapid comparison between multiple pairs of trees employs the Day (1985) linear-time algorithm.
Functions
RobinsonFouldsMatching(): Matched splits, intended for use withVisualizeMatching().
Normalization
RobinsonFoulds()is normalized against the total number of splits that are present.InfoRobinsonFoulds()is normalized against the sum of the phylogenetic information of all splits in each tree, treated independently.
References
Day WHE (1985).
“Optimal algorithms for comparing trees with labeled leaves.”
Journal of Classification, 2(1), 7–28.
doi:10.1007/BF01908061
.
Robinson DF, Foulds LR (1981).
“Comparison of phylogenetic trees.”
Mathematical Biosciences, 53(1-2), 131–147.
doi:10.1016/0025-5564(81)90043-2
.
Smith MR (2020).
“Information theoretic Generalized Robinson-Foulds metrics for comparing phylogenetic trees.”
Bioinformatics, 36(20), 5007–5013.
doi:10.1093/bioinformatics/btaa614
.
Smith MR (2022).
“Robust analysis of phylogenetic tree space.”
Systematic Biology, 71(5), 1255–1270.
doi:10.1093/sysbio/syab100
.
See also
Display paired splits: VisualizeMatching()
Other tree distances:
HierarchicalMutualInfo(),
JaccardRobinsonFoulds(),
KendallColijn(),
MASTSize(),
MatchingSplitDistance(),
NNIDist(),
NyeSimilarity(),
PathDist(),
SPRDist(),
TreeDistance()
Examples
# For BalancedTree, PectinateTree, as.phylo:
library("TreeTools", quietly = TRUE)
balanced7 <- BalancedTree(7)
pectinate7 <- PectinateTree(7)
RobinsonFoulds(balanced7, pectinate7)
#> [1] 4
RobinsonFoulds(balanced7, pectinate7, normalize = TRUE)
#> [1] 0.5
VisualizeMatching(RobinsonFouldsMatching, balanced7, pectinate7)
 InfoRobinsonFoulds(balanced7, pectinate7)
#> [1] 13.90209
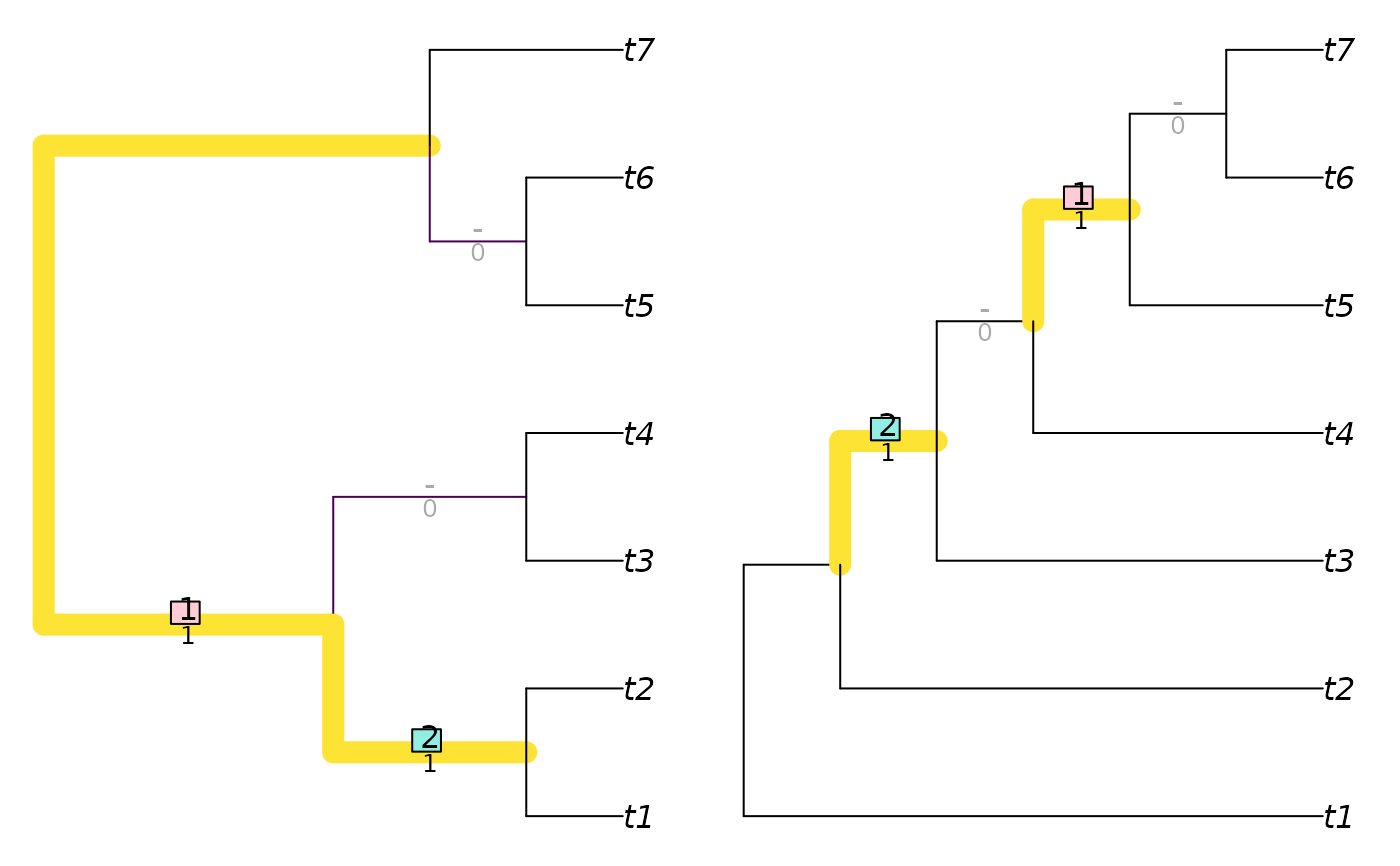
VisualizeMatching(InfoRobinsonFoulds, balanced7, pectinate7)
InfoRobinsonFoulds(balanced7, pectinate7)
#> [1] 13.90209
VisualizeMatching(InfoRobinsonFoulds, balanced7, pectinate7)